今や機械学習と言えばほぼディープラーニング、つまり多層のニューラルネットワークを指すようになった。ニューラルネットワークによる識別手法や生成手法で溢れる昨今だが、それらとは別の用途にニューラルネットワークを活用する例も増えてきている。
NeRF: Neural Radiance Fields
NeRFはECCV 2020で発表された論文 NeRF: Representing Scenes as Neural Radiance Fields for View Synthesisで提案されたNovel View Image Synthesis(多視点画像を手がかりに未知の視点画像を合成する)手法。
NeRFはとても高品質な未知視点画像を合成できるので、それを応用するとリアルな3D自由視点映像を作成できる。
GitHubで公式のソースコードも公開されている↓
https://github.com/bmild/nerf
NeRFの仕組みの概要
NeRFは、あるシーン(3次元空間)を複数の視点から撮影した100枚程度の画像(とカメラパラメータ)を使ってニューラルネットワークを学習することで、シーンの連続した光(Radiance)の分布をニューラルネットワークで近似・補間して保持する。
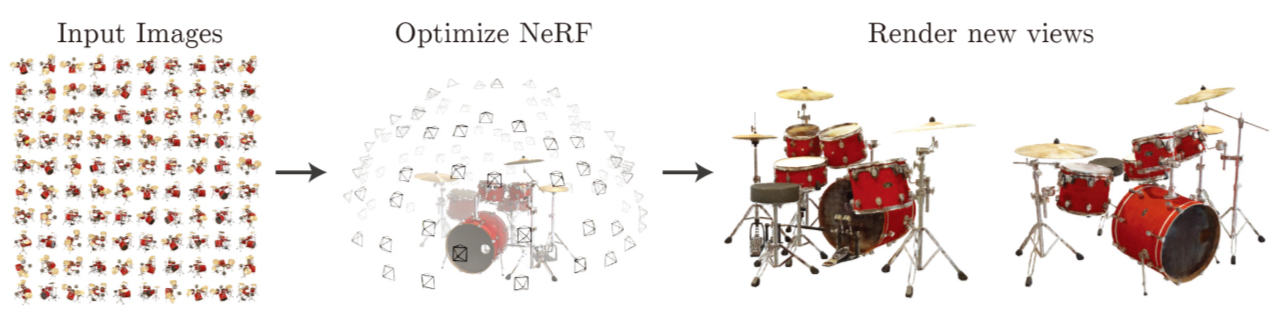
NeRFの学習
3Dシーンを複数視点から撮影した画像とカメラパラメータでニューラルネットワークを学習する
特定の3Dシーンに最適化されたこのニューラルネットワークは、視線(カメラ)の情報を入力すると、シーンをその視線から見た(撮影した)光景の2D画像を出力するレンダラーとして機能する。
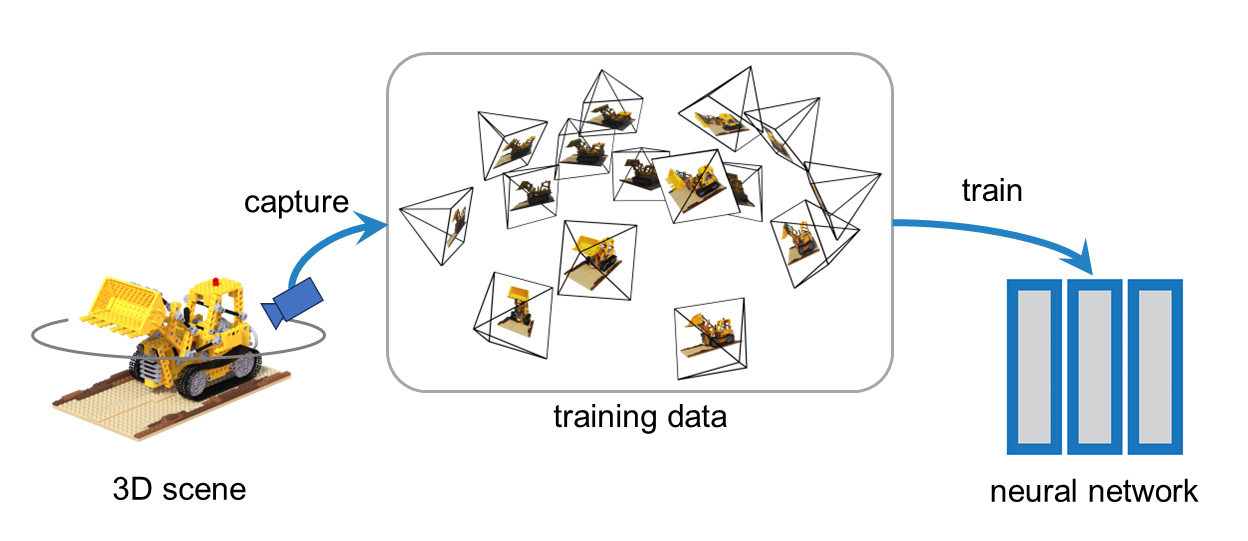
NeRFのレンダリング
ニューラルネットワークに視線をクエリ(ray casting)して、2D画像1ピクセルの色を計算する
NeRFでのニューラルネットワークの役割
NeRFでのニューラルネットワークの役割は、連続的な世界(3Dシーン)から得た離散的なサンプル(複数視点画像)を使って、元の世界を表現する連続関数を得ること。
離散的なサンプルから連続関数を復元する補間問題と捉えると、識別手法や生成手法と同様にディープラーニングが得意とする課題だ。
NeRFでの学習は、通常の機械学習のような汎化性能を求めてあらゆるシーンに対応するわけではなく、特定シーンのみへの最適化を目指す。ある意味で過剰適合(overfitting)な学習。
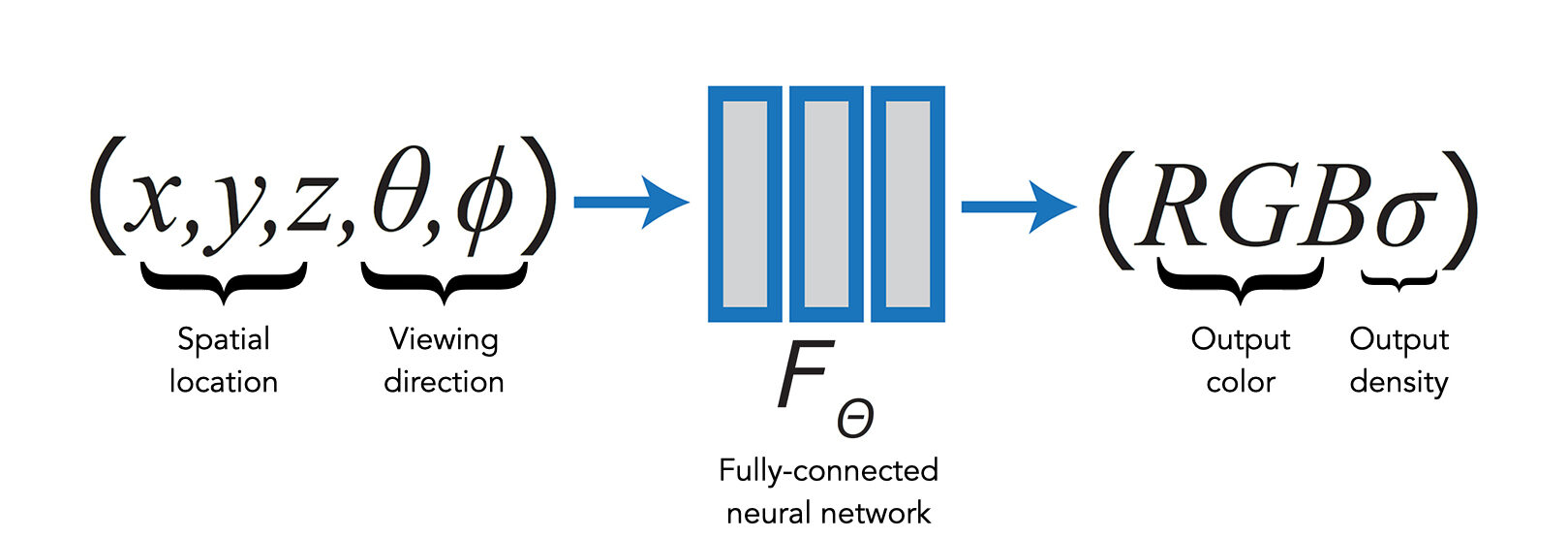
NeRFで使用するニューラルネットワークはごく標準的な全結合ニューラルネットワーク(MLP:多層パーセプトロン)で、シーン内のある点の位置、シーンを観測する視線方向を入力とし、視線方向から見たその点の色、その点の密度を出力する。
x, y, z:シーン内のある点の3次元位置座標
θ, φ:視線方向 (θ: yaw, φ: pitch)RGB:視線方向から見たシーン内の点(x, y, z)の色
σ:シーン内の点(x, y, z)の密度:パラメータ(重み)Θを学習済みの全結合ニューラルネットワーク(MLP:多層パーセプトロン)
1つの入力クエリに対して出力されるのは1点の情報だけなので、シーンをカメラで撮影したかのような2D画像をレンダリングするには、カメラの画角に対応するピクセル解像度分の視線方向を作成(投影)する必要があり、1つの視線ごとに交差した全点(視線上の全点)の色を積分することになる。(つまり、ナイーブに計算するとかなり重い処理)
NeRFでレンダリングできる画像
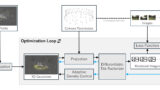
NeRFは、元の画像セットには含まれない視点から見た画像もリアルに復元することができ、視線を滑らかに変化させて連続した画像をレンダリングすれば、実際にカメラで移動撮影したかのようなリアルな自由視点映像を作成できる。
元の画像セットには含まれない未知の視点から見た光景をとてもリアルにレンダリングでき、このNovel View Image Synthesis(未知視点画像を合成する)タスクの性能の高さでNeRFは大きな注目を浴びた。
「見た目」を重視した3次元復元
Structure from MotionやMulti-View Stereoなど、従来の3次元復元手法が3Dの「形状」の復元を主眼としていたのに対し、NeRFは3Dの「見た目」の復元を得意とする。シーンに降り注いだ光を受けた物体の鋭く指向性のある反射、透明な物体の屈折など、シーン内の光の情報をそのまま復元・保持でき、見た目上のリアリティが高いため、特に映像分野での活用が期待される。
では、NeRFを実現する基本アイディアについて詳しく見て行こう。
シーンをNeural Radiance Fieldsで表現する
NeRFでは、シーン(3次元空間)のRadianceをNeural Fieldsで表現・保持する。
と言っても、そもそもRadianceとNeural Fieldsとは何なのか。
Radiance (放射輝度)とは?
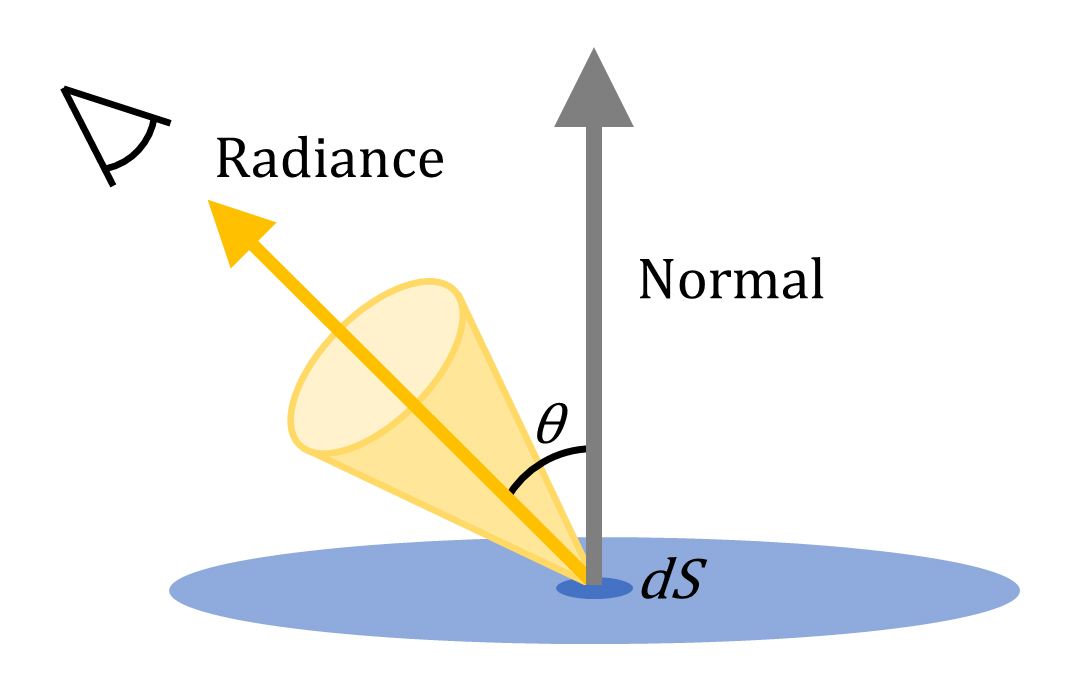
Radiance (放射輝度)はもともと物理で使われる用語で、放射源の表面からある方向へ放出される放射束(Radiance Flux)を表す、面積と向きに依存する物理量のこと。
CG分野では特に、面積がほぼ省略され、(レンダリング画像の1ピクセルに相当する)微小面積(dS)から「ある方向」へ放出される光の量を表し、目(カメラ)に届く光の算出に使用される指向性を持つベクトル量のこと。
NeRFでのRadianceの意味はさらに大雑把で、単に目(カメラ)に届く色を表している。
なので、ここでのRadianceは「指向性を持ち、視線方向に依存する色」程度の理解で大丈夫。要するに、
-
Radiance:見る角度によって色が変化する点(物体表面)の質感を表現できるベクトル量
ということ。NeRFの最適化(学習)に使用するデータは普通のRGB画像なので、画像に写っている「色」以上にリッチで厳密な情報はそもそも扱えない。
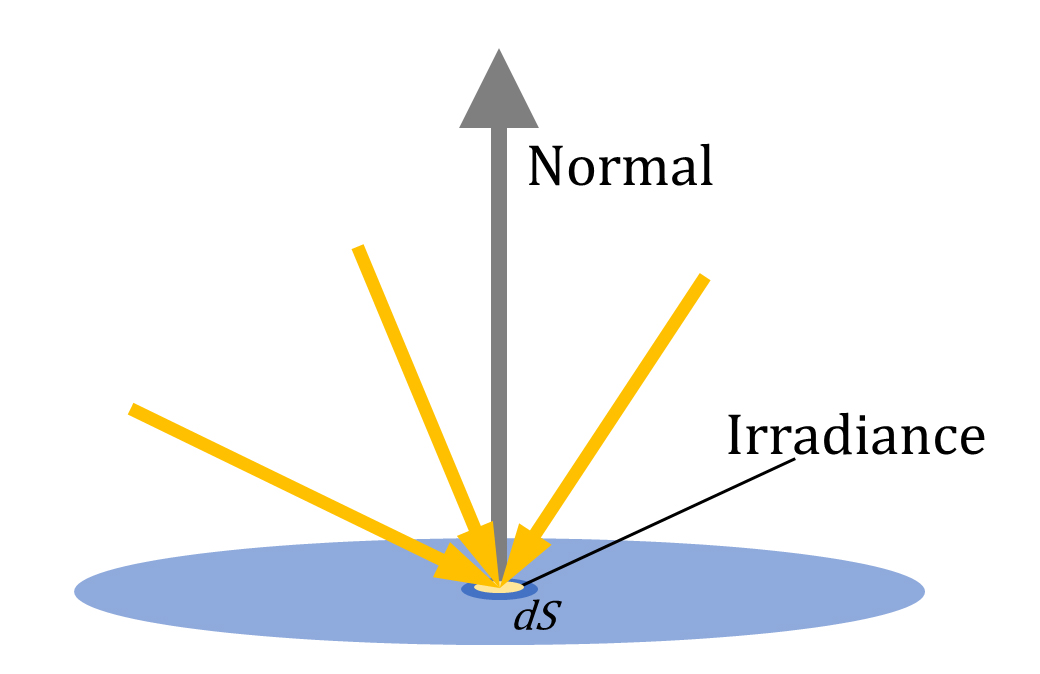
ちなみに、ある面から目に届く光の量をRadianceと呼ぶのとは逆に、単位面積あたりに降り注ぐ光の量はIrradiance (放射照度)と呼び、こちらは指向性の無い量を表す。(響きがややこしいですね)
Neural Fields (ニューラル場)とは?
Neural Fields (ニューラル場)とは、連続した値の分布をニューラルネットワークを用いて近似する手法の総称で、ある空間中のベクトル量の分布を表現・保持するVector Fields (ベクトル場)をニューラルネットワークを用いて実現したもの。
Vector Fields (ベクトル場)の可視化

Vector Fieldsが座標値を入力するとベクトル値を出力する関数と定義されるのと同様に、Neural Fieldsは座標値を入力するとベクトル値を出力するニューラルネットワークと定義される。
Neural Radiance Fields
Neural Radiance Fieldsは、座標値を入力するとベクトル値 Radianceが出力されるNeural Fieldsということ。冒頭でも説明したように、Neural Radiance Fieldsは3次元位置x=(x, y, z)と視線方向(θ, φ)を入力とし、色c=(r, g, b)と密度σを出力するMLP(多層パーセプトロン)と定義される。
実装上、視線方向(θ, φ)は3次元直交座標系(デカルト座標系)の単位ベクトルdと表現され、MLP(多層パーセプトロン)は以下のように定式化される。
Neural Radiance Fieldsの定式化
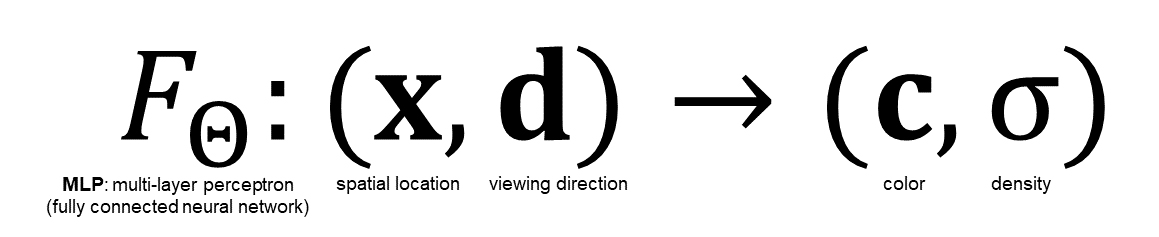
:重みΘを学習したMLP(多層パーセプトロン)
x:シーン内のある点の3次元位置座標
d:シーンを観測する視線方向c:視線方向から見たシーン内の点xの色
σ:シーン内の点xの密度
このMLP(多層パーセプトロン) が連続した3Dシーン表現を近似し、入力された位置xと視線方向dを、対応する色cと密度σにマッピングできるように重みΘを最適化(学習)することになる。
Neural Fieldsを使用するメリット
既存のVector Fieldsの実装と比べて、Neural Fieldsによる表現には以下のメリットがある。
- データがコンパクト
- 帰納バイアスによる出力の滑らかさ
- 定義域の次元数を容易に拡張できる
- 微分可能
空間を格子状に離散化してベクトル量を保持する等の従来のVector Fieldsの実装では、離散解像度の次元数乗でデータ量が膨れ上がってしまう。それに比べ、Neural Fieldsは遥かに少ないデータ量で高解像度の情報を表現・保持できる。
帰納バイアス (inductive bias)とは、使用するアーキテクチャやアルゴリズムによって生じる制約のこと。ニューラルネットワークにはその構造自体に出力の滑らかさを保つ制約が働くことが知られており、その性質がNeRFの高品質なレンダリング結果に寄与している。
この帰納バイアスが働くことで人手による「滑らかさ」の調整が不要なため、ハイパーパラメーターを1つ減らせる。
通常、Vector Fieldsの定義域の次元を増やすにためは、各問題固有の事情を考えて慎重に設計する必要がある。一方ニューラルネットワークは、入力層のパラメーターを増やすだけで定義域の次元を増やすことができ、柔軟に定義域を拡張することができる。
Neural Fieldsはニューラルネットワークで構成されているので、通常のディープラーニングと同様に微分値を利用した勾配法によって最適化(学習)できる。
レンダリング結果を微分してニューラルネットワークを最適化(学習)するという点で、NeRFは微分可能レンダリングの側面を持つ。
その他、昨今のニューラルネットワークライブラリの充実がNeural Fieldsの実装を容易にしている面もある。
Neural Radiance Fieldsのレンダリング
特定の3Dシーンに最適化されたNeural Radiance Fieldsから2D画像をレンダリングする処理は、Volume Renderingの手法を用いて画像の1ピクセルごとに独立して行われる。
Volume Renderingとは?
Volume Renderingとは、主にボクセル(voxel)等の3Dボリュームデータを2D画像にレンダリングする手法の総称。
ボリュームデータとは?
物体の表面だけを表現し内部が空っぽのハリボテのようなポリゴンデータと違い、ボリュームデータは物体の外形だけでなく内部構造の情報も保持するデータ形式。そのため、ボリュームデータは物体内部を透視して内部の密度の分布を視覚的に表す用途でよく使われる。
医療分野では、CTやMRIで撮影された2Dスライス画像を合成した3D表示などで活用されている。
CG分野では特に、霧や煙・雲など、透過性のある不定形な物体のレンダリングによく使われる。ボリュームデータは、表面の境界がハッキリせず、内部の密度が一定でない物体(現象)を表現するのに適している。
近年ではボリュームデータを扱うためのオープンな規格OpenVDBがCG分野で普及しつつある。

UnityではボリュームデータをTexture3Dというボクセル形式で扱いますね。
volume ray casting
Volume Renderingの中でも、最も古典的でシンプルなレンダリング手法がvolume ray casting (またはvolume ray marching)。
ray castingはray tracingに代表される、視点からray(光線)を逆に辿る(backword)レンダリングの最も基礎的な方法。
通常のポリゴンデータを対象としたray castingでレンダリング画像1ピクセルの色を得るには、視点からカメラ投影面の画像ピクセルに相当する方向へrayを飛ばし、最も手前(視点側)のrayと物体(ポリゴン)の交差点を計算して1ピクセルの色を得る。1ピクセルにつき1つのrayが必要で、レンダリング画像の解像度分のrayを飛ばすことになる。
ray castingによるポリゴンデータのレンダリング
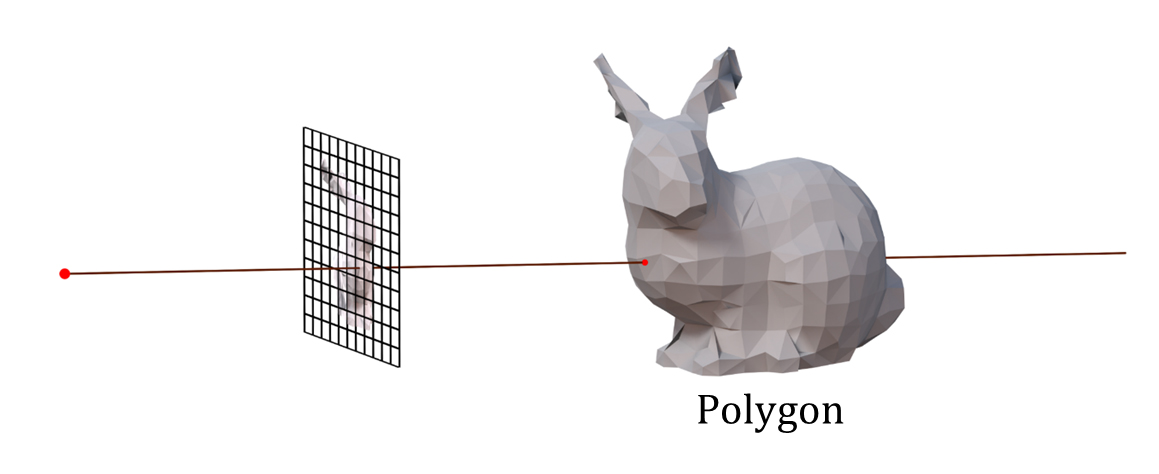
ボリュームデータを対象としたvolume ray castingの場合は、rayと物体表面の交差点だけでなく、rayが通過する物体(ボリューム)内部の通過範囲全ての色を積分(加算)して1ピクセルの色を得る。
volume ray castingによるボリュームデータのレンダリング
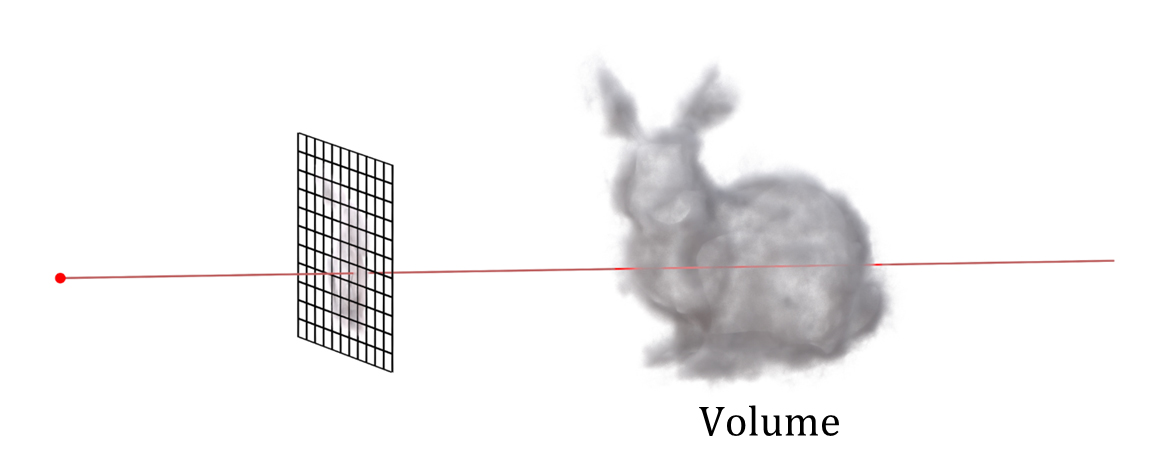
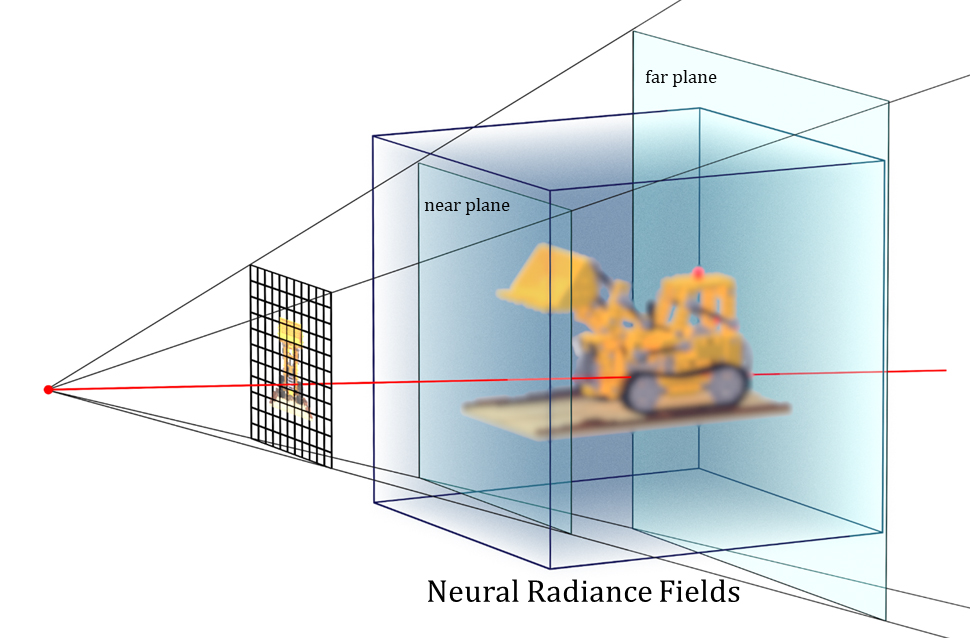
実装上は、視点からの距離の下限を定義するnear plane(近境界)と、上限を定義するfar plane(遠境界)を設けて色の積分区間(描画範囲)を制限し、積分を何らかの方法で離散的に解くことになる。
near plane / far planeでvolume ray castingの色の積分区間を定義する
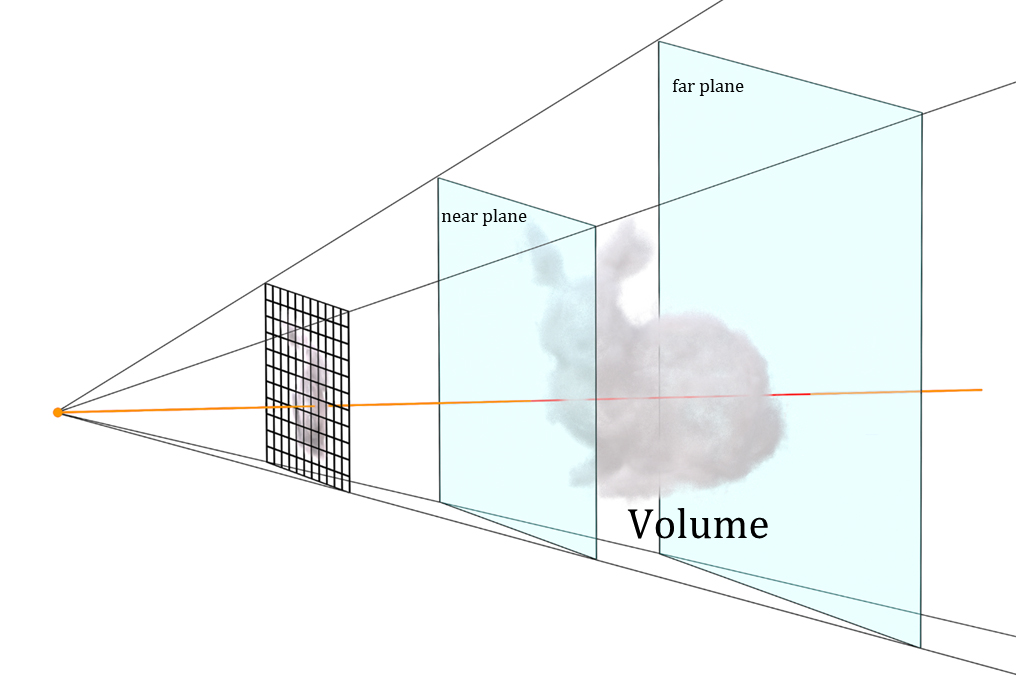
Neural Radiance Fieldsから2D画像をレンダリングする
NeRFのレンダリングの仕組みは、volume ray castingでのボリュームデータを、ニューラルネットワークによるNeural Radiance Fieldsにそのまま置き換えたような構成。
rayから1ピクセルの色を求める
ボリュームデータのvolume ray castingと同様に、レンダリング画像1ピクセルにつき1つ(1つの方向)ずつrayを飛ばしてピクセルの色を求める。
3次元空間(Neural Radiance Fields)上の1点の色を求める
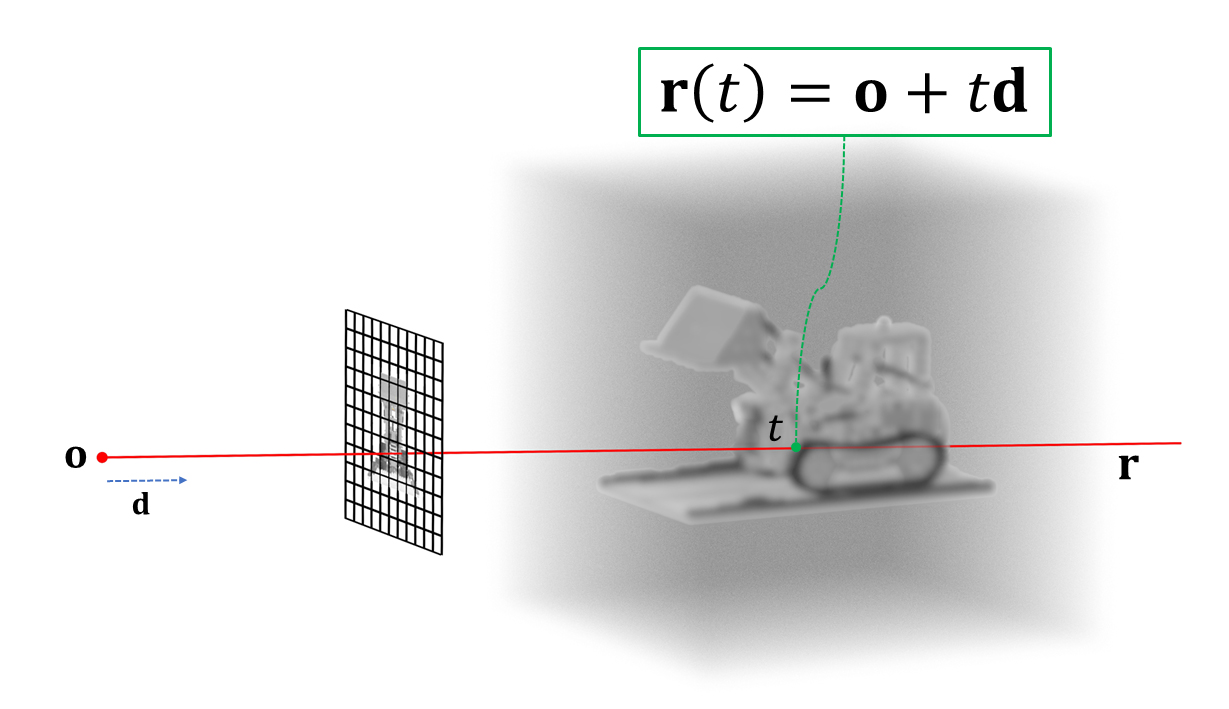
rayの開始点となる視点の位置座標をo、rayを飛ばす方向(視線方向)をd、rayが視点oから視線方向dへどれだけ進むかをパラメータt (スカラー)で表すと、ray上の任意の点(3次元位置座標)は以下の関数で表せる。
ray castingではお馴染みのこの式を図示すると以下のようになる。
視点oから方向dへ飛ぶray r上の任意の点𝐫(𝑡)
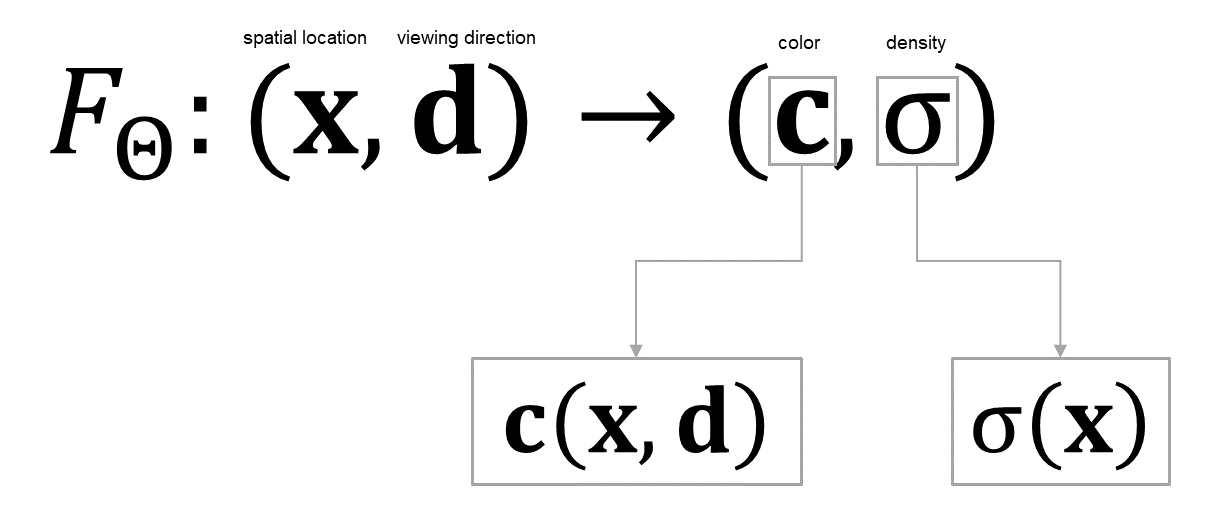
この関数で決定される位置座標𝐫(𝑡)を、Neural Radiance Fieldsを定式化した関数の入力位置座標xに代入、視線方向dはそのまま入力することで、色cと密度σが得られる。
関数は1つのニューラルネットワークだが、以降の説明を分かりやすくするために出力ごとに別関数へ分解し、色(Radiance)を求める関数c、密度を求める関数σと表記する。
𝐜(𝐱, 𝐝):視線方向から見た点xの色を求める関数 σ(𝐱):点xの密度を求める関数
色の積分
これら2つの関数の位置座標xに𝐫(𝑡)を代入するとray上の1点の色cと密度σが得られる。しかしこれはあくまで3次元空間上の1点の情報だけなので、レンダリング画像1ピクセルの色を得るにはNeural Radiance Fields上のrayが通過する範囲全ての情報を積分する必要がある。
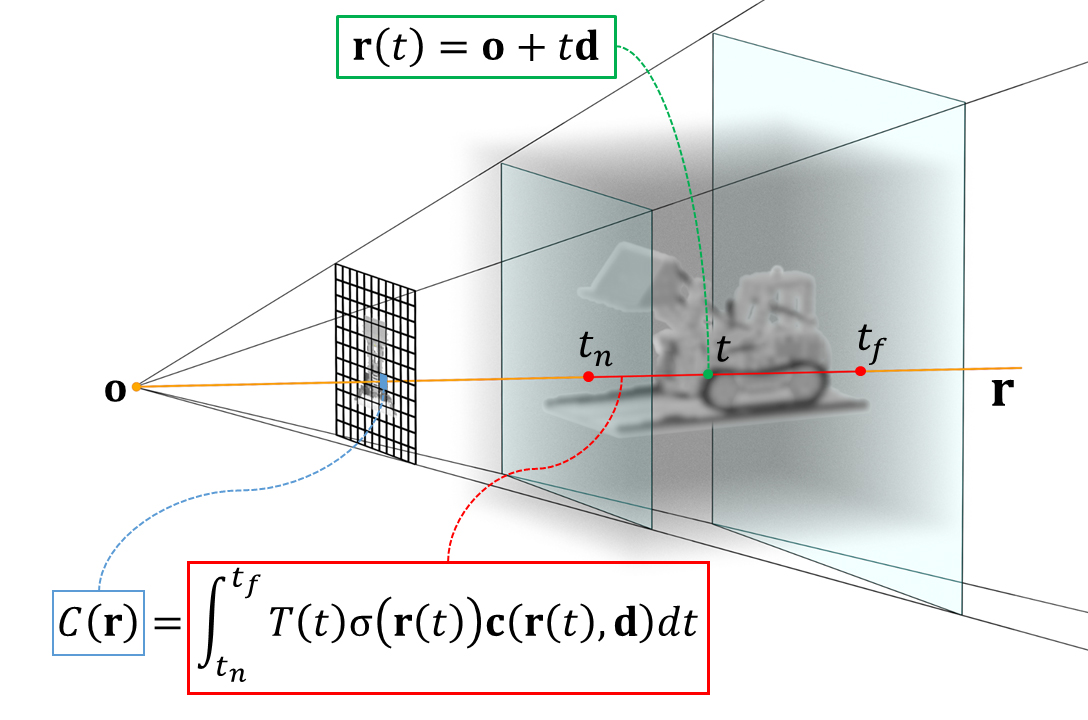
near plane / far planeで定義した積分区間を[,
]と表記すると、レンダリング画像1ピクセルの色𝐶(𝐫)を求める積分は以下のように定義される。
レンダリング画像の1ピクセル(1つのray)の色を求める積分の定義
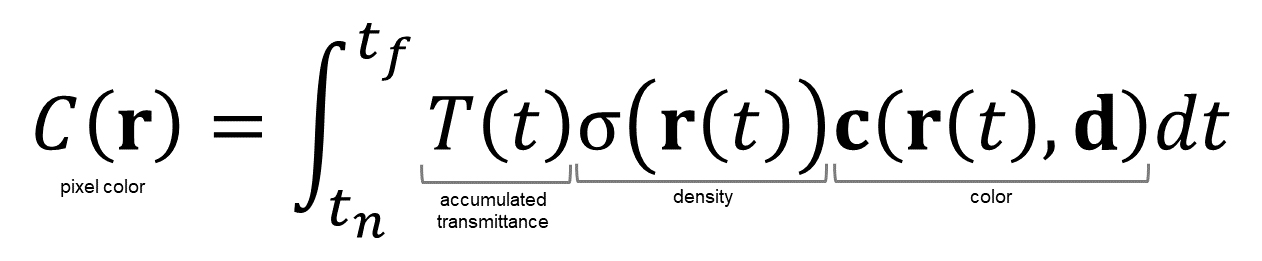
ここで、関数𝑇(𝑡)はをからtにおける累積透過率(Accumulated Transmittance)で、rayが
からtの区間を通過する際に遮られる確率、つまり視点へ届く光が何らかの物体に遮られて減衰する現象を表している。
密度が濃いところほど光が遮られて0に近づく。(つまり光の透過率が低くなる)
rayの からtまでの累積透過率を表す関数
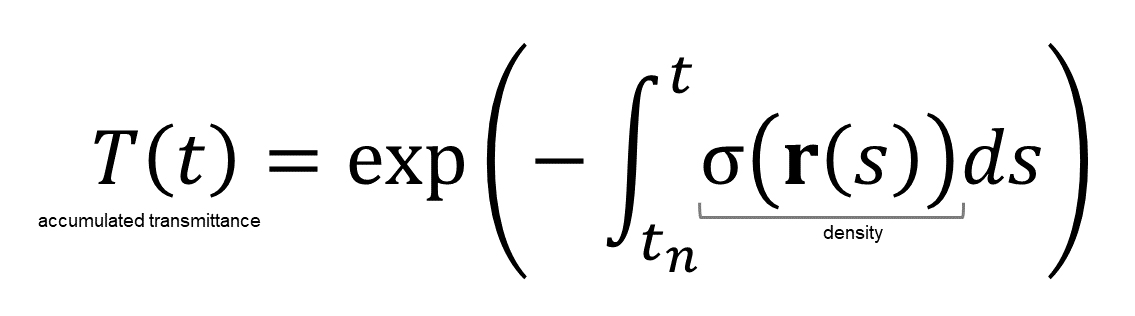
視点から見たから点𝐫(𝑡)までの密度σが高いと累積透過率𝑇(𝑡)の値が小さくなり、点𝐫(𝑡)の色の影響が小さくなる。
ここまでの定義を図示すると以下のようになる。
色の積分の離散化
実装では、積分区間[,
]からN個の点をサンプリングして離散的に処理する。サンプリングは一定間隔ではなく、以下で定義された範囲から一様分布
に基づいたランダムサンプリングでサンプリング点
を決定する。
サンプリングされたN個のの集合について密度
と色
を出力して積算することで1ピクセルの色
が求まる。
色の積分計算の離散化
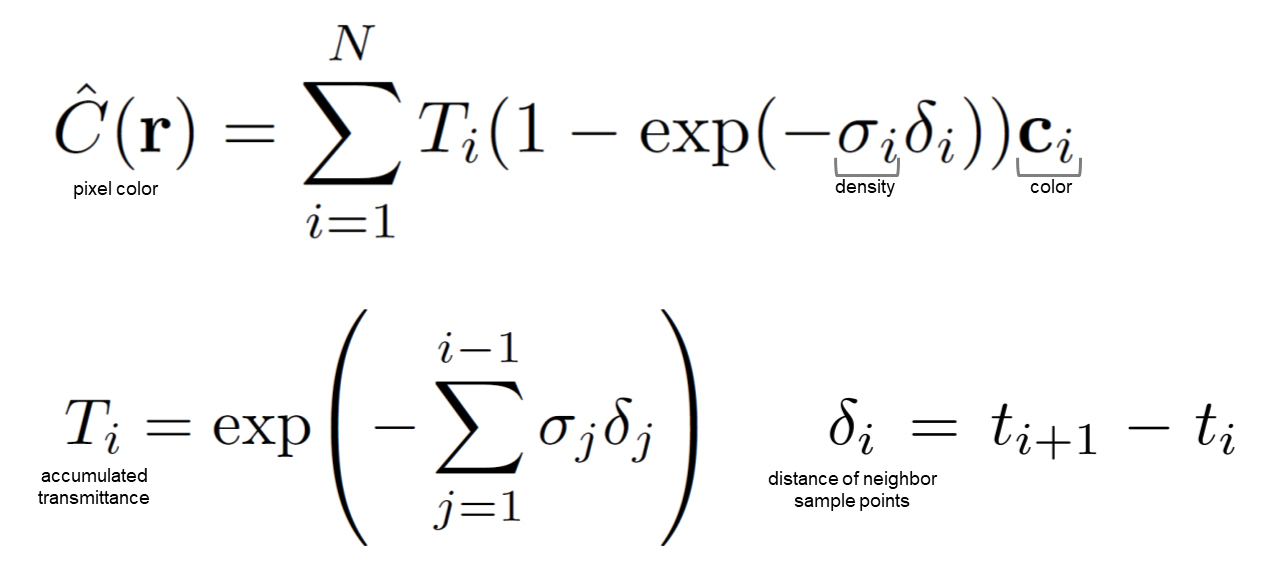
この積分を2D画像の全ピクセルについて計算することで1枚の画像がレンダリングされる。
NeRFの学習データ
Neural Radiance Fieldsの最適化(学習)に必要なデータは、対象シーンを複数視点から撮影した100枚程度の画像と、それら画像それぞれに対応するカメラパラメーター。
カメラパラメーターとは?
カメラパラメーターとは、カメラをピンホールカメラモデルと呼ばれる単純な投影モデルで近似する際のパラメーターのこと。
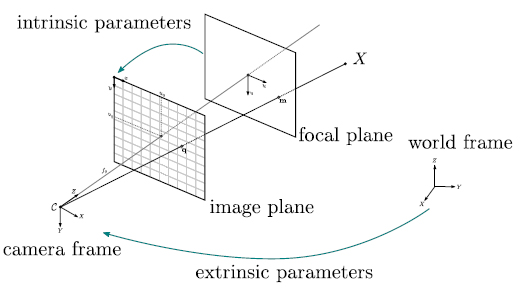
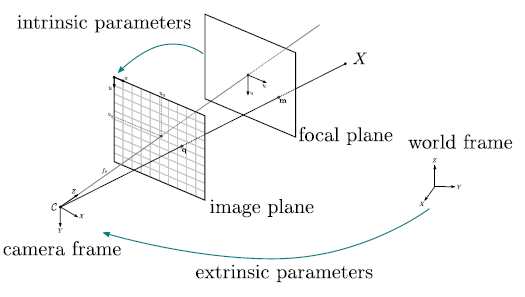
カメラの射影行列(3D→2D)をintrinsic parameters(内部パラメーター)とextrinsic parameters(外部パラメーター)の2つの行列で表し、内部パラメーターは3D→2Dの投影関係、外部パラメーターはカメラの3D空間での位置・向きを定義する。
以下の図は、3D空間の座標をカメラで撮影して2Dのスクリーン座標へ投影する様子を表している。
複数視点画像
NeRFのシーン例でよく見かけるLEGOのブルドーザーは、BlenderでレンダリングされたCG画像。Blenderから複数視点画像をレンダリングする際に同時にカメラパラメータもJSONで書き出されている。
CGだとレンズによる歪みの無い理想的なピンホールカメラモデルによる画像を作成できるので、扱う問題がシンプルになりますね。
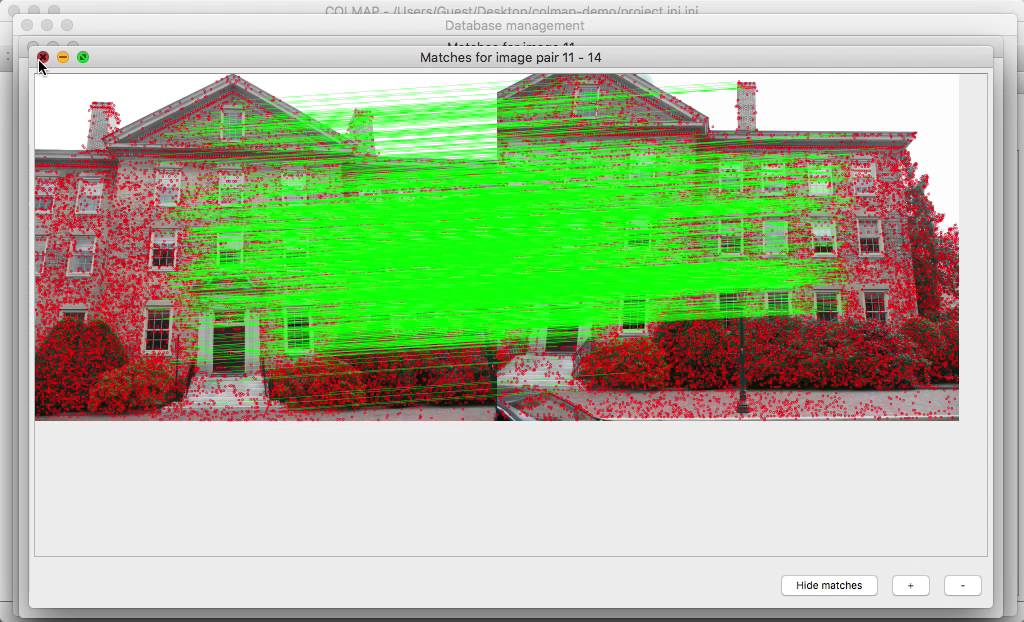
実写画像を使用する場合には、撮影済みの複数画像からSfMツールのCOLMAPを使ってカメラパラメーターを推定して使用する。
品質向上・効率化のための工夫
ここまでの定義だけでNeural Radiance Fieldsを実装すると、それらしい画像はレンダリングできるがディティール(高周波成分)がぼやけてしまう。
理論上ニューラルネットワークは任意の連続関数を近似できるが、NeRFの入力は位置座標と視線方向だけの低次元情報なため、出力が低周波成分へ収束してしまう帰納バイアスによって高周波成分を捉えられず自然画像の色と形状を上手く表現できないのだ。
また、レンダリング時のサンプリング・積分処理は3Dシーン内の密度分布の粗密に関わらず一定の数をサンプリングしているため処理効率が悪く、計算速度が遅い。
これらの問題に対して、NeRFでは以下2つのアプローチを行っている。
- Positional Encoding
- Hierarchical Volume Sampling
Positional Encodingによる品質向上 (高周波成分を捉える)
自然画像の高周波成分を捉えるために、Positional Encoding関数で、低次元の入力(位置座標、視線方向)を高次元空間に埋め込んでからニューラルネットワークへ入力する。(Transformerで使われるPositional Encodingとは使用目的が異なる)
L:マッピングする次元数を決定するパラメーター
位置座標と視線方向の各値を[-1, 1]に正規化してpに代入し、位置座標はL = 10、視線方向はL = 4で高次元空間へマッピングする。
これは要するに、入力(位置座標、視線方向)をフーリエ級数展開して周波数成分ごとに明示的に分解し、次数L-1(L-1項目)までを個別の次元の値として採用するということ。
Positional Encodingによって高周波成分を捉えたレンダリングが可能になる。
1番左が正解画像、続いて3枚がNeRFの構成要素別レンダリング結果
2枚目:フルモデル、3枚目:視線依存無し、4枚目:Positional Encoding無し
位置座標にはかなり高い次数(高周波成分)まで必要だが、視線方向については割と少ない次数(低周波成分)までで十分ということらしい。
Hierarchical Volume Samplingによる効率化
3Dシーン内の密度分布の偏りを考慮し、疎な領域のサンプリングは省略して、物体の境界付近など色が急激に変動する領域や物体が密集する領域だけを重点的にサンプリングしてレンダリングするHierarchical Volume Samplingという戦略をとる。
Hierarchical Volume Samplingは、3Dシーンを単一のNeural Radiance Fieldsで表現するのではなく、同一構造のNeural Radiance Fieldsを2つ用意し、粗い(coarse)ネットワークと細かい(fine)ネットワークで3Dシーンを表現して、サンプリング対象を戦略的に決定する。学習時にはこれら2つのネットワークを同時に最適化することになる。
- Coarse Network:シーン中の大まかな色・密度の分布を得るための粗いネットワーク
- Fine Network:詳細な色・密度を得るための細かいネットワーク
レンダリング画像1ピクセル(1つのray)の評価について、まずCoarse Networkにrayを飛ばして個の点をサンプリングして色と密度を出力し、それを手掛かりにFine Networkの同一ray上の密度が高い(より情報量が多い)点を重点的に
個サンプリングする。
これを実現するためのCoarse Networkでの1つのrayの評価(離散積分)は、以下のように重みによる色
の加重和に書き換えた式で定義される。
ここで、重みを以下のように正規化すると、rayに沿った区分ごとに定数となる確率密度関数(probability density function)が得られる。
Coarse Networkから得た分布で個のサンプリング点を生成し、
個のサンプリング点と
個のサンプリング点を合わせた
+
個のサンプリング点を使ってFine Networkを評価することで最終的なピクセルの色を得る。
これによって、対象の密度に応じた効率的なレンダリングができる。
NeRFの損失関数
NeRFの学習の目標は、色と密度を出力するMLP(多層パーセプトロン)の最適化であり、学習データの画像と同一視点でレンダリングした画像の差が最小となるパラメータΘを獲得すること。この最適化のための損失関数は以下で定義される。
Coarse NetworkとFine Networkの2つのNeural Radiance Fieldsのピクセル値と、同一カメラパラメーターで位置合わせされた教師画像のピクセル値の2乗誤差を最小化する。
Neural Radiance Fieldsのネットワーク構造
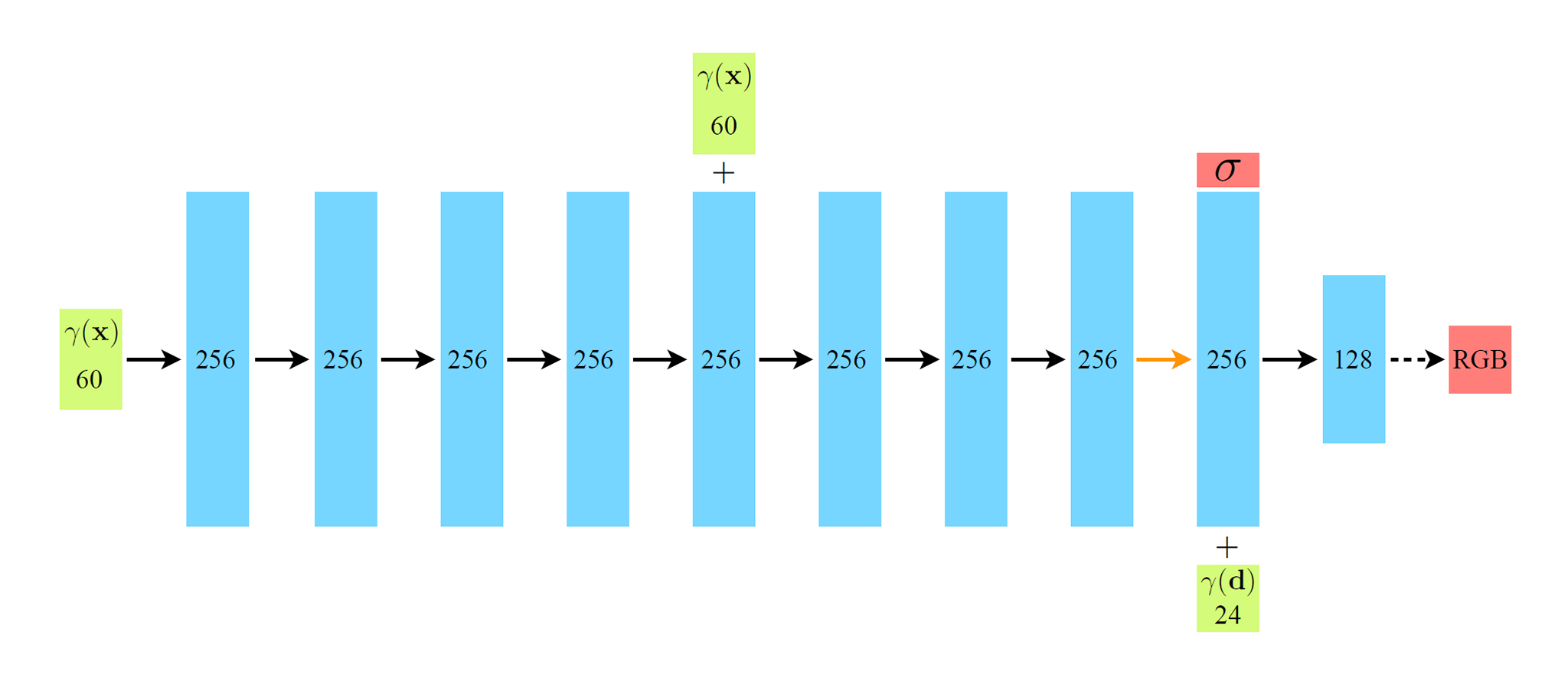
最終的に、NeRFで使われるニューラルネットワークは以下のような構造となる。一般的なディープラーニング手法と比べて極めて少ないレイヤーで構成されており、必要な学習画像は100枚程度とかなり少ない。
全てのレイヤーが全結合層、各ブロック内の数字はベクトルの次元数を表す
緑ブロック:入力ベクトル
青ブロック:中間隠れ層ベクトル
赤ブロック:出力ベクトル黒矢印:ReLU活性化関数のあるレイヤー
オレンジ矢印:活性化関数の無いレイヤー
黒点線矢印:シグモイド活性化関数のあるレイヤー
+:ベクトルの連結
入力位置座標のPositional Encoding (γ(x))をそれぞれ256チャネルの8層の全結合ReLUレイヤーを通過させ、5層目の活性化関数にも入力位置座標を連結する(スキップ接続)。
9層目で密度σ(非負であることを保証するためにReLUで整流)と256次元の特徴ベクトルを出力し、視線方向のPositional Encoding (γ(d))と連結して、最後の層(シグモイド活性化関数)で視線方向dのrayから見た位置xの色を出力する。
その後の発展・応用
NeRFは高品質な自由視点映像をコンパクトなデータ量で表現できるが、最適化(学習)処理とレンダリング処理がどちらも重く、最適化済みのNeural Radiance Fieldsを編集しにくい等、欠点も多々ある。
NeRFが発表されて以降、欠点を改善した手法が数多く発表されている→ Awesome Neural Radiance Fields
気軽に試せるツールもいくつか→ Luma AI, Nerfstudio, BlenderNeRF
参考図書
今のところ、NeRFの解説が日本語で読める書籍は以下4冊。
CVIMチュートリアルのNeRF関連記事はコンピュータビジョン最前線 Autumn 2022の記事の再編版。CGは数学でできているではNeRFの解説の中でVolume Renderingが説明される。




cvpaper.challengeのメタサーベイが図も多くて分かりやすいけど、CG分野への理解の乱暴さがやや気になる。
最近の新手法
Siggraph 2023で3D Gaussian Splattingという新手法が発表されて新たなブームが起こっている。
視線方向ごとに全然別の画像を与えて最適化すると、見る方向によって別の絵に見えるアートが作れるね↓
Another experiment with Gaussian Painters ✨🎨
By optimizing 3D Gaussian Splattings over separate images at several viewpoints, it is possible to get a Steganography effect! Three paintings are hidden in those gaussian splats https://t.co/wwKzYoZdg5 pic.twitter.com/QyDPVARCfM
— Alex Carlier (@alexcarliera) September 2, 2023

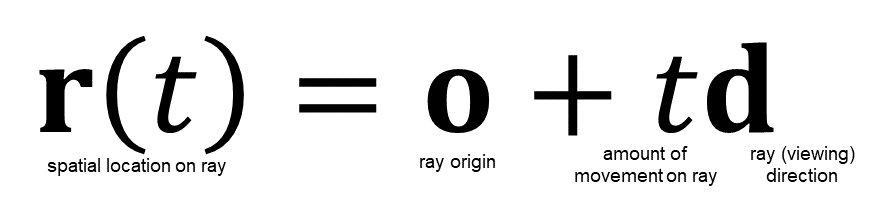
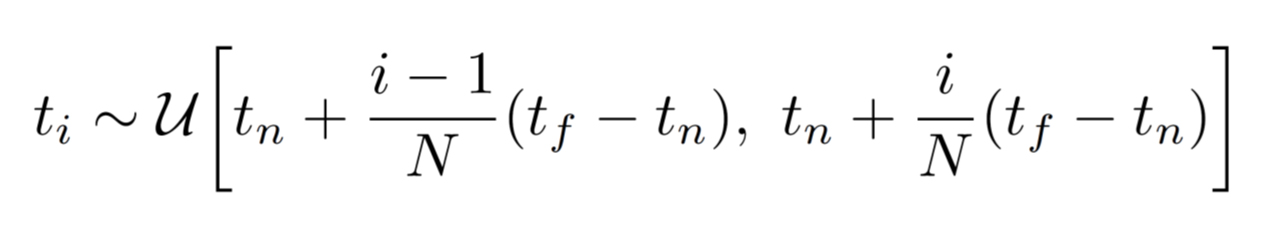

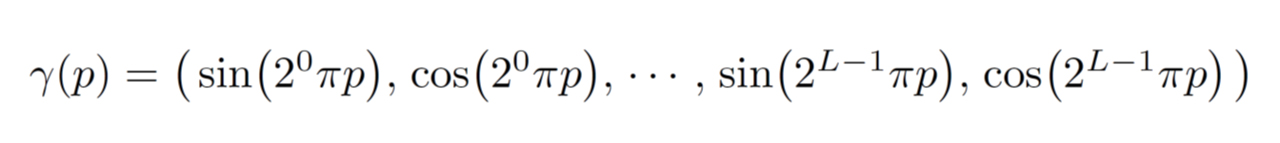

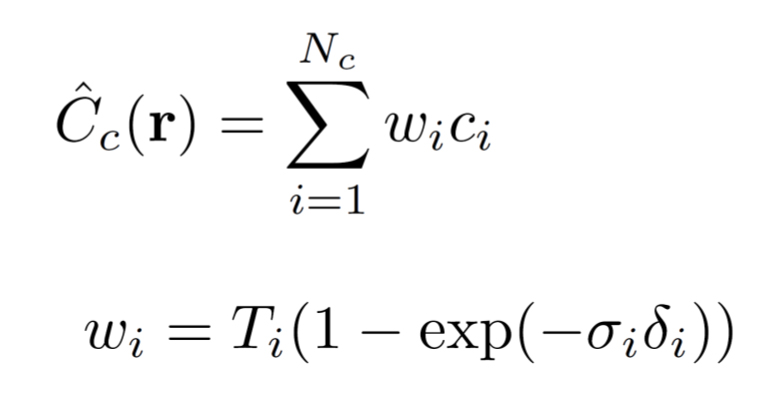
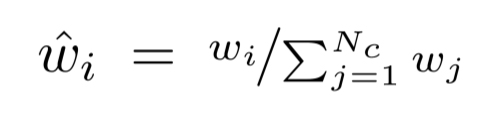


コメント