2次元の画像から3次元の情報を復元するプログラムを本格的に実装してみようと思って、まずはOpenGVから触り始めたんだけど、オイラの基礎知識が乏し過ぎて苦戦中。
まだOpenGVに同梱されているtestコードをいじってみている段階。オイラはこの分野の基本的な用語の知識が欠けているので、OpenGV独自の抽象化APIで使われる言葉との区別もつかず、公式ドキュメントを読むだけでだいぶ苦労する。(ドキュメント自体はそれほど文量多くないけど)
ということで、まずはこの分野で使われる言葉の意味をちゃんと知っておこうと思います。この分野は「エピポーラ幾何(Epipolar geometry)」とか「エピ極線幾何学」って呼ぶんですかね。
ライブラリの公式ドキュメントは英語なので、英語表記と日本語表記の対応もちゃんとおさえておく。OpenMVGの公式の機能一覧やcameras, multiviewの解説と図がシンプルで分かりやすかったので引用しながらまとめる。
数学的な定義よりも画像処理での用途寄りに書いていきますが、間違ってたらごめんなさい。(ご指摘いただけると有難い)
スポンサーリンク
Pinhole Camera Model：ピンホールカメラモデル
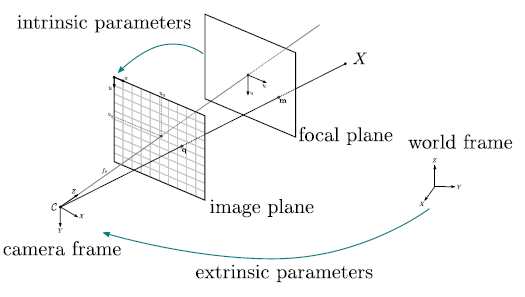
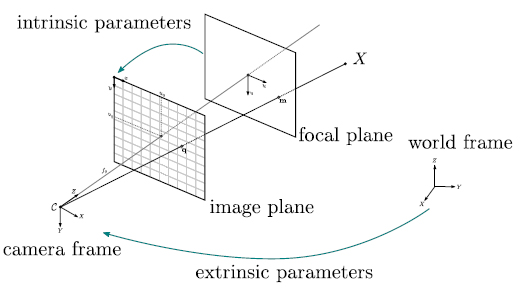
カメラは図のようなピンホールカメラモデルと呼ばれる単純な投影モデルで近似することができ、2D→3D復元の様々なアルゴリズムは基本的にこのモデルに基づいている。
ピンホールカメラモデルでは、カメラの射影行列(3D→2D)をintrinsic parameters(内部パラメータ)とextrinsic parameters(外部パラメータ)の2つの行列で表す。内部パラメータは3D→2Dの投影関係、外部パラメータはカメラの3D空間での位置・向きを定義する。
上の図は、3Dのワールド座標をカメラで撮影することで2Dのスクリーン座標へ投影する様子を表している。
Homography：ホモグラフィ
画像認識におけるHomographyとは、2D空間同士の射影変換のこと。
(一般的には、射影変換全般をHomographyと呼ぶ)
図で赤く示されているような3D空間上のある平面について、2つのカメラ
このような、平面の座標系から別の平面の座標系へ変換する2D→2Dの射影変換行列がHomography行列H(3×3の行列)となる。
OpenCVだとcv::findHomography関数を使えば2枚の画像間のHomography行列を推定することができる↓
http://qiita.com/wakaba130/items/b566f15a4f2cf1ce414f
Homography行列の算出には、対応点が最低でも6点(全て同一平面上なら4点)必要だそうです。
https://qiita.com/tomoaki_teshima/items/dc49a1431562da4da436
Fundamental Matrix：基礎行列
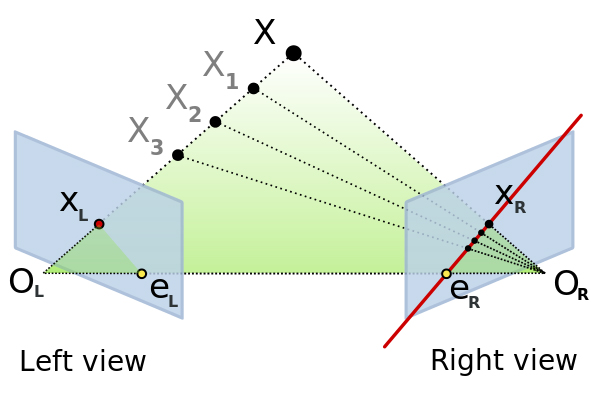
Fundamental Matrix(基礎行列)は同一のシーンを撮影している2つのカメラ画像の関係を表す3×3の行列。カメラ画像中の点をもう1つのカメラ画像のスクリーン座標へ変換する2D-2Dの座標変換を行うことができる。基礎行列Fと表記されたりします。Fundamental Matrix(基礎行列)は2焦点テンソル(bifocal-tensor)とも呼ばれるとか。
OpenCVならcv::FindFundamentalMat関数を使えば2枚の画像からFundamental Matrix(基礎行列)を推定することができるらしい。(8点アルゴリズム)
基礎行列の歌なんてのもあるようですよ↓
Essential Matrix：基本行列
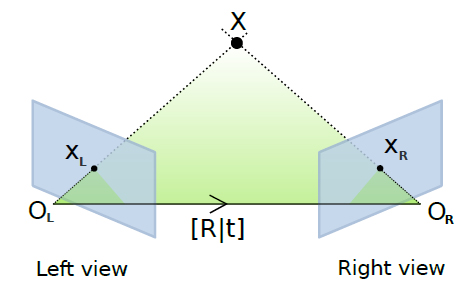
図のように、2つのカメラ
Essential Matrix(基本行列)は、このRとtを1つにまとめた4×4の行列![[R|t]](https://s0.wp.com/latex.php?latex=%5BR%7Ct%5D&bg=ffffff&fg=000&s=0&c=20201002)
ここで、行列
基本行列Eは基礎行列Fに内部パラメータKを与えることで導出できます。
OpenCVだと、このEssential Matrix(基本行列)はcv::findEssentialMat関数を使えば算出できます。これは、いわゆる5点アルゴリズム(five-point algorithm)というやつで、計算するには対応点が5点以上必要となります。
また、cv::recoverPose関数、cv::decomposeEssentialMat関数を使ってEssential Matrix(基本行列)を回転行列Rと並進ベクトルtへ分解することもできます。
スポンサーリンク
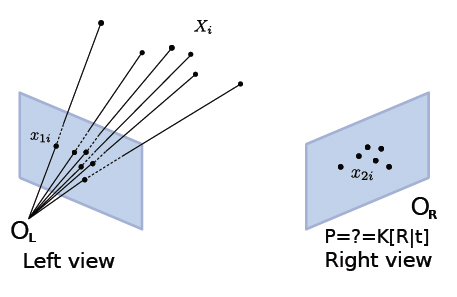
Resection/Pose Estimation：キャリブレーション/姿勢推定
Camera Resectionとは、いわゆるカメラキャリブレーションのことです。
カメラのキャリブレーション、カメラの姿勢を推定するにはワールド座標とスクリーン座標の3D-2Dの点の対応情報が必要です。推定したカメラパラメータを用いて3D→2Dの変換を行い、事前に与えたスクリーン座標との差を算出します。この差(残留誤差)が最小となるよう最適化することでカメラパラメータを求めます。
Triangulation：三角測量
CG屋は”Triangulation“と言うと三角形分割と訳してしまいそうですが、ここでは三角測量を意味します。
カメラの位置・姿勢、内部パラメータ、画像間の2D-2Dの対応の情報が既知であれば、三角測量の原理に基づいて対応点の三次元座標を推定することができます。
OpenCVには三角測量による三次元座標の計算を行うためのcv::triangulatePoints関数があります。
感想
とりあえず、今オイラが理解している情報を書いてみた。(後半ちょっと雑になりましたが)
今後も随時加筆修正していこうと思う。
こうしてまとめて見ると、OpenCVはその分野についての用語を知っていれば大体使えるようにAPIが上手く抽象化されているのが分かる。画像認識について体系的に学んだ人にとっては扱うのチョロいんだろうなぁ。
逆に、適切に抽象化されたAPIを使っているとその分野の体系が分かってくるとも言えるのかな。学ぶ上での教材としてこういうのは大事かも。これはエンジニア(プログラマ)流の学び方かもしれない。
追記：すごくいいまとめ記事↓
http://qiita.com/ykoga/items/14300e8cdf5aa7bd8d31
http://news.mynavi.jp/series/cv_future/006/
http://news.mynavi.jp/series/cv_future/008/
http://news.mynavi.jp/series/cv_future/009/
http://news.mynavi.jp/series/cv_future/010/
参考書
調べていたら、どうやらMultiple View Geometry in Computer Visionという洋書があるらしく、この書籍には2D→3D復元技術のことが体系的にまとまっているようです。
でもお高いです。。。
追記：本書の一部はPDFで無料公開されている↓
http://www.robots.ox.ac.uk/~vgg/hzbook/
追記：最近出たこちらの書籍はそのものズバリ、3次元コンピュータービジョンを体系的に学べるようになっています。かなり教科書っぽいので、それなりに覚悟は必要です↓
ピンホールカメラモデルとキャリブレーションについてはOpenCV 2 プログラミングブックのChapter4の2.1にもサンプルコードも合わせて解説が載っている。サンプルコードはサポートサイトから。
http://qiita.com/tunepolo/items/76058121238be386bb21
2D-3D対応からのカメラ位置・姿勢の推定する、いわゆるPnP問題(Perspective-n-Pont Problem)をOpenCVで解く方法についてはOpenCV3対応のこちらが詳しい↓
同様にサンプルコードはサポートページからダウンロードできる。
追記：OpenCV3公式のカメラキャリブレーションと3次元復元の解説ドキュメントの日本語訳を掲載しているサイトを見つけた↓
http://labs.eecs.tottori-u.ac.jp/sd/Member/oyamada/OpenCV/html/py_tutorials/py_calib3d/py_table_of_contents_calib3d/py_table_of_contents_calib3d.html
2019年6月 追記：SSII 2019でカメラキャリブレーションのチュートリアルがあった↓
スポンサーリンク
コメント