もう1年以上前になりますが、書籍「イラストで学ぶ ディープラーニング」を購入して少しずつ読み進めていたのです。↓

ところが、読み進めている途中で壁にぶち当たりました。この書籍、途中からどんどん数式率が上がって行き、あんまりイラストで教えてくれなくなるんですよ(笑)
数式が苦手だから「イラストで学ぶ」に期待していたのですが、考えが甘かったようです。
載っているサンプルコードは各種Deep Learningライブラリの使い方なので、肝心の仕組みは当然隠蔽されていて、そこから仕組みを理解するのは難しい。(ライブラリの使い方を覚えられる分実践的なんだけどね)
なので、実装しながら仕組みを理解していく方針に切り替えることにした。
ということで、こちらの書籍に頼ることにしました↓ (すぐ書籍買っちゃう)

Pythonのサンプルコードと、書籍の正誤表はGitHubにある↓
https://github.com/oreilly-japan/deep-learning-from-scratch
https://github.com/oreilly-japan/deep-learning-from-scratch/wiki/errata
これでディープラーニングを作れる(笑)
書籍のサンプルコードはPythonですが、そこは慣れたUnity(というかC#)環境に置き換えて学ぼうと思い、PythonのNumPyに代わる数値計算ライブラリを探していたのでした。
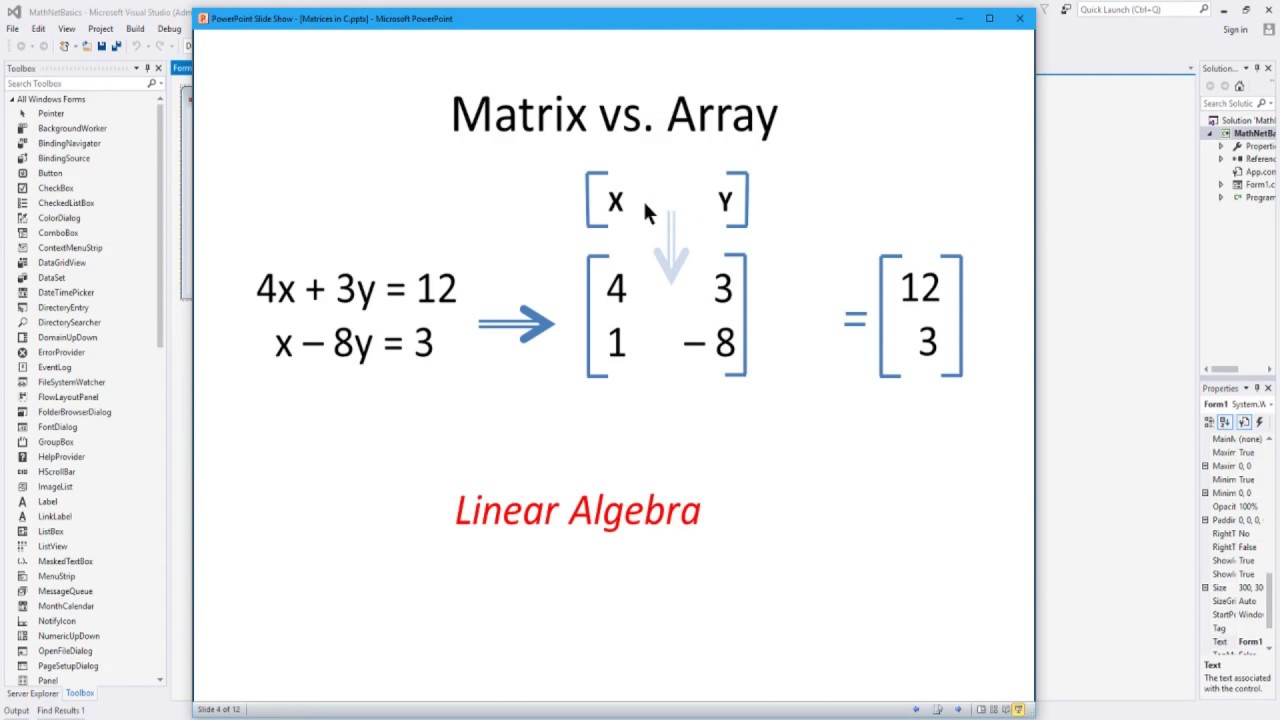
で、Math.NET Numerics導入後に少し調べたら、似た発想の人がいた↓
http://tnakamura.hatenablog.com/entry/2016/12/05/perceptron
http://tnakamura.hatenablog.com/entry/2016/12/08/sigmoid-relu-softmax
http://tnakamura.hatenablog.com/entry/2016/12/15/mnist
http://tnakamura.hatenablog.com/entry/2016/12/16/three-layer-neural-network
http://tnakamura.hatenablog.com/entry/2017/01/30/loss-function
http://tnakamura.hatenablog.com/entry/2017/02/08/numerical-differentiation
http://tnakamura.hatenablog.com/entry/2017/02/10/numeric-gradient
http://tnakamura.hatenablog.com/entry/2017/02/15/gradient-descent
http://tnakamura.hatenablog.com/entry/2017/02/20/gradient-simplenet
https://github.com/snaga/DeepLearning_C_Sharp
せっかくなので実装の参考にさせていただこう。Math.NET Numericsの使い方を知るのに良いサンプルだ。
Unity上で動作の仕組みを可視化できたら最高なんだが、そこまで行けるだろうか。
2019年 追記:今ならMath.NET Numericsじゃなくて、このNumSharpを使った方が良いと思う↓

パーセプトロン、ニューラルネットワークのイメージ
書籍とは関係ないけど、パーセプトロン、ニューラルネットワークの働きをビジュアル化するとこんなイメージらしい↓
色んなアルゴリズムをこんな感じで可視化できると理解が捗るだろうなぁ。
関連記事
Pylearn2:ディープラーニングに対応したPythonの...
Managing Software Requirements...
書籍『OpenCV 3 プログラミングブック』を購入
Math.NET Numerics:Unityで使える数値計...
ポリゴンジオメトリ処理ライブラリ『pmp-library (...
書籍『絵はすぐに上手くならない』読了
サンプルコードにも間違いはある?
YOLO (You Only Look Once):ディープ...
WinSCP
網元AMIで作ったWordpressサイトのインスタンスをt...
FCN (Fully Convolutional Netwo...
オープンソースの物理ベースGIレンダラ『appleseed』
書籍『クラッシャー上司 平気で部下を追い詰める人たち』読了
Unityで画面タッチ・ジェスチャ入力を扱う無料Asset『...
RefineNet (Multi-Path Refineme...
ブログが1日ダウンしてました
Caffe:読みやすくて高速なディープラーニングのフレームワ...
書籍『鈴木さんにも分かるネットの未来』読了
Web経由でRaspberry PiのGPIOを操作したい
Kornia:微分可能なコンピュータービジョンライブラリ
オープンソースの取引プラットフォーム
OpenCVのバージョン3が正式リリースされたぞ
マルコフ連鎖モンテカルロ法
仮想関数
ベイズ推定とグラフィカルモデル
書籍『ROSプログラミング』
透明標本
OANDAのfxTrade API
FacebookがDeep learningツールの一部をオ...
Amazon EC2ログイン用の秘密鍵を無くした場合の対処方...
書籍『ゴジラの工房 若狭新一造形写真集』
WordPressプラグインの作り方
Cartographer:オープンソースのSLAMライブラリ
DUSt3R:3Dコンピュータービジョンの基盤モデル
ニューラルネットワークと深層学習
Google XML Sitemap Generatorプラ...
UnityのTransformクラスについて調べてみた
機械学習に役立つPythonライブラリ一覧
SSD (Single Shot Multibox Dete...
2D→3D復元技術で使われる用語まとめ
OpenCVで顔のモーフィングを実装する
ArUco:OpenCVベースのコンパクトなARライブラリ



コメント